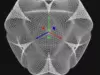
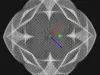
Harmonic Hyperqube – Algorithmic 3D ModelGeometry Details + Vertices: 49,284, Triangles: 16,428

The Harmonic Hyperqube unites two timeless ideas, the geometry of higher dimensions and the proportions of harmonic resonance. With 49k vertices and 16k triangles, this algorithmic model transforms the abstract hypercube into a tangible archetype of symmetry and vibration. A reminder that mathematics resonates across dimensions, linking structure, sound, and space.

Who

Rooted in the works of mathematicians like Ludwig Schläfli (1850s), who studied higher-dimensional polytopes, and modern researchers in geometry and theoretical physics. The hypercube (or tesseract) is a central concept in mathematics, computer science, and physics.

What

The Harmonic Hyperqube is a 3D structure generated through harmonic algorithms, inspired by the geometry of the hypercube (n-dimensional cube).A hypercube generalizes the idea of a square (2D) and cube (3D) into higher dimensions (4D and beyond). By fusing harmonics (patterns of frequency and proportion) with hypercube geometry, the design symbolizes balance between structure and resonance.

When

The hypercube concept was formalized in the 19th century, during the rise of higher-dimensional mathematics. Harmonic design principles, however, trace back to ancient Greece, where Pythagoras linked mathematics, geometry, and musical harmony. This model is a modern computational synthesis of both traditions.

Where

In mathematics, they are studied in topology, graph theory, and dimensional geometry. In physics, hypercubes appear in theories of space-time, string theory, and multidimensional modeling. In culture, tesseracts are found in sci-fi literature, art, and symbolic philosophy.

Why

The hypercube challenges our perception of space, showing us how geometry extends beyond visible dimensions. By integrating harmonics, the Hyperqube becomes a metaphor for order, resonance, and multidimensional symmetry. It demonstrates how mathematics connects the seen and unseen, the audible and visual, the finite and infinite.